周期Tの超関数f(x)は次のように複素フーリエ級数展開できるのであった：

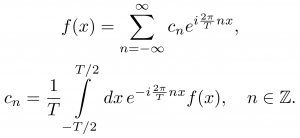
この展開においてTが非常に大きい状況(T→∞)を考えれば、du = 1/Tは非常に小さな値となり、また周波数u = n/Tはどんな実数値も取れるようになると考えられる：

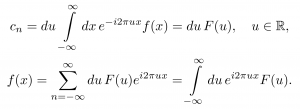
このF(u)を「f(x)のフーリエ変換」という：

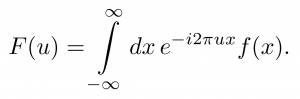
また，逆にF(u) から元のf(x) を求める操作

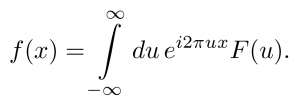
をフーリエ逆変換という．

フーリエ級数展開は有限区間(例えば[－T/2, T/2]) 上で定義された関数を周期的に拡張たものを級数展開していたのであるが、このTが無限大になったことから、元の超関数f(x)には「有限区間」とか「周期性」とかいった制約がなくなる。